Mupad Syntax:
- Code: Alles auswählen
plot( // Code by Yukterez:
// Vektor [x,y] [x2,y2] Radius:
// ASTERISK5
plot::Line2d([0,0], [0,r], r=0..1),
plot::Line2d([0,0], [+r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], r=0..1),
plot::Line2d([0,0], [-r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], r=0..1),
plot::Line2d([0,0], [+r*cos(3*PI/10),-r*sin(3*PI/10)], r=0..1),
plot::Line2d([0,0], [-r*cos(3*PI/10),-r*sin(3*PI/10)], r=0..1),
// PENTAGON
plot::Line2d([+r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], [0,r], r=0..1),
plot::Line2d([-r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], [0,r], r=0..1),
plot::Line2d([+r*cos(3*PI/10),-r*sin(3*PI/10)], [+r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], r=0..1),
plot::Line2d([-r*cos(3*PI/10),-r*sin(3*PI/10)], [-r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], r=0..1),
plot::Line2d([-r*cos(3*PI/10),-r*sin(3*PI/10)], [+r*cos(3*PI/10),-r*sin(3*PI/10)], r=0..1),
// PENTAGRAMM
plot::Line2d([-r*cos(3*PI/10),-r*sin(3*PI/10)], [0,r], r=0..1),
plot::Line2d([-r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], [+r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], r=0..1),
plot::Line2d([-r*cos(3*PI/10),-r*sin(3*PI/10)], [+r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], r=0..1),
plot::Line2d([+r*cos(3*PI/10),-r*sin(3*PI/10)], [-r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], r=0..1),
plot::Line2d([+r*cos(3*PI/10),-r*sin(3*PI/10)], [0,r] r=0..1),
// SPITZEN
plot::Point2d([0,r], r=0..1),
plot::Point2d([+r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], r=0..1),
plot::Point2d([-r*cos(PI/2-2*PI/5),+r*sin(PI/2-2*PI/5)], r=0..1),
plot::Point2d([+r*cos(3*PI/10),-r*sin(3*PI/10)], r=0..1),
plot::Point2d([-r*cos(3*PI/10),-r*sin(3*PI/10)], r=0..1))
Formel:
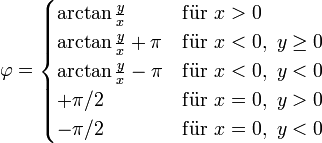
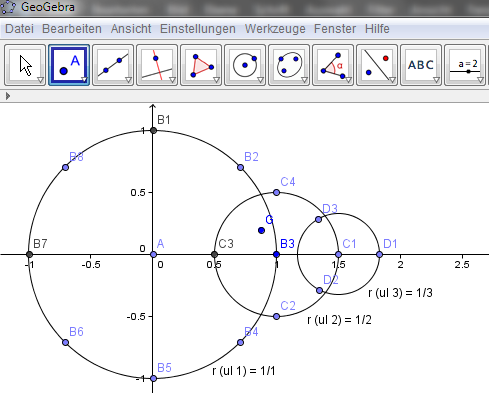
Der Vollkreis muss in 90° (π/2 Radianten) Abschnitte aufgeteilt werden. Anwendung der Formel:
x = r*cos(φ); y = r*sin(φ)

Für eine Ellipse wird ein Faktor vor x oder y gesetzt: Ellipse.png & Kreis.png
Sechsstern:
- Code: Alles auswählen
plot( // Code by Yukterez:
plot::Circle2d(r, [0,0], r=0..1),
// Vektor [x,y] [x2,y2] Radius:
// ASTERISK6
plot::Line2d([0,0], [0,+r], r=0..1),
plot::Line2d([0,0], [0,-r], r=0..1),
plot::Line2d([0,0], [+r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], r=0..1),
plot::Line2d([0,0], [-r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], r=0..1),
plot::Line2d([0,0], [+r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], r=0..1),
plot::Line2d([0,0], [-r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], r=0..1),
// HEXAGON
plot::Line2d([-r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], [0,-r], r=0..1),
plot::Line2d([+r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], [0,+r], r=0..1),
plot::Line2d([+r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], [+r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], r=0..1),
plot::Line2d([-r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], [-r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], r=0..1),
plot::Line2d([+r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], [0,-r], r=0..1),
plot::Line2d([-r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], [0,+r], r=0..1),
// HEXAGRAMM
plot::Line2d([+r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], [-r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], r=0..1),
plot::Line2d([-r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], [0,-r], r=0..1),
plot::Line2d([+r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], [0,+r], r=0..1),
plot::Line2d([+r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], [0,-r], r=0..1),
plot::Line2d([-r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], [+r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], r=0..1),
plot::Line2d([-r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], [0,+r], r=0..1),
// SPITZEN
plot::Point2d([0,r], r=0..1),
plot::Point2d([0,-r], r=0..1),
plot::Point2d([+r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], r=0..1),
plot::Point2d([-r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], r=0..1),
plot::Point2d([+r*cos(PI/2-PI/3),-r*sin(PI/2-PI/3)], r=0..1),
plot::Point2d([-r*cos(PI/2-PI/3),+r*sin(PI/2-PI/3)], r=0..1))

Beim 7-Stern geht es im selben Prinzip weiter:
- Code: Alles auswählen
// yukterez.enabled.io
plot( plot::Ellipse2d(r,r, [0,0], r=0..1),
plot::Point2d( [0, +r], r=0..1),
plot::Point2d( [+r*cos(PI/2-2*PI/7), +r*sin(PI/2-2*PI/7)], r=0..1),
plot::Point2d( [+r*cos(PI/2-4*PI/7), +r*sin(PI/2-4*PI/7)], r=0..1),
plot::Point2d( [+r*cos(-5*PI/14), +r*sin(-5*PI/14)], r=0..1),
plot::Point2d( [-r*cos(+5*PI/14), +r*sin(-5*PI/14)], r=0..1),
plot::Point2d( [-r*cos(PI/2-4*PI/7), +r*sin(PI/2-4*PI/7)], r=0..1),
plot::Point2d( [-r*cos(PI/2-2*PI/7), +r*sin(PI/2-2*PI/7)], r=0..1))

usw. usf.





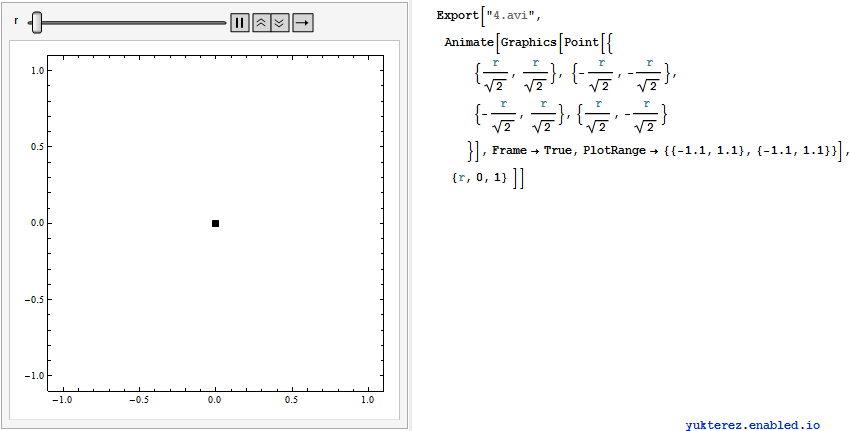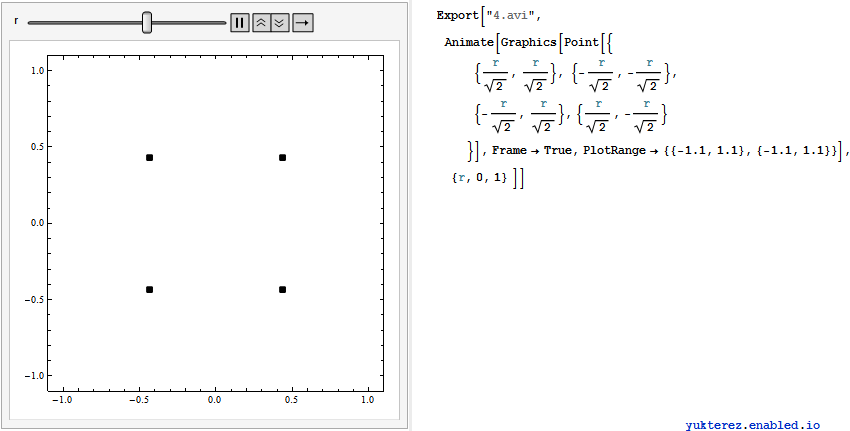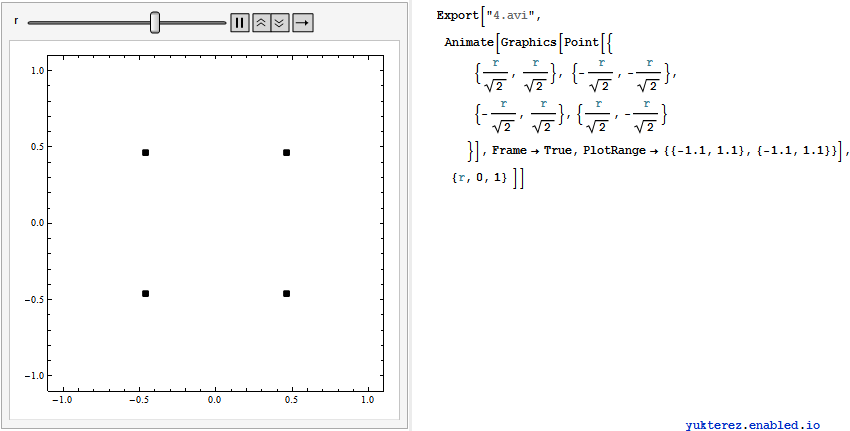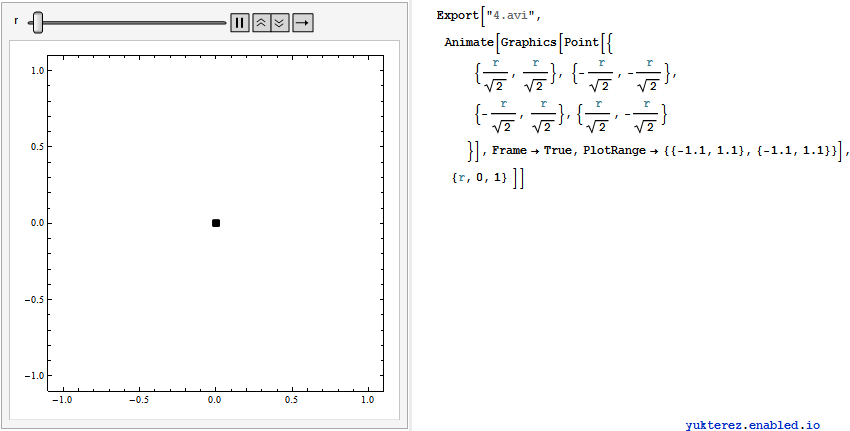





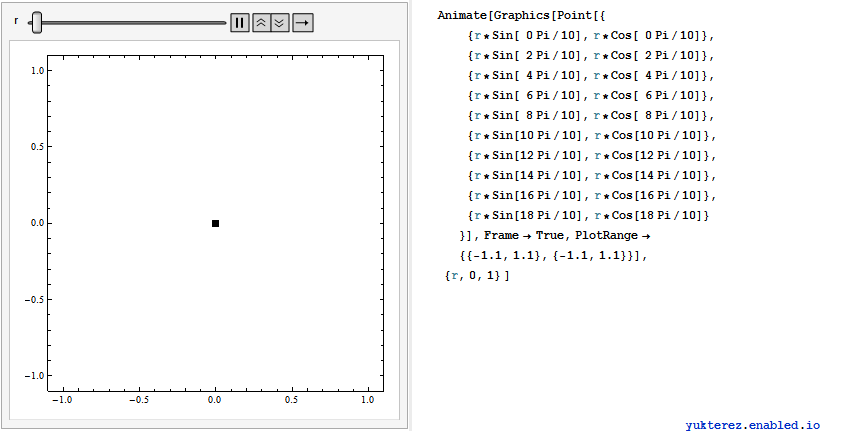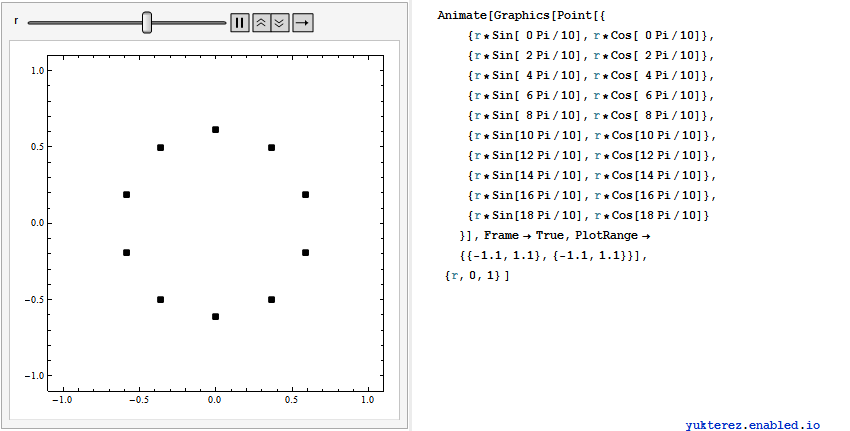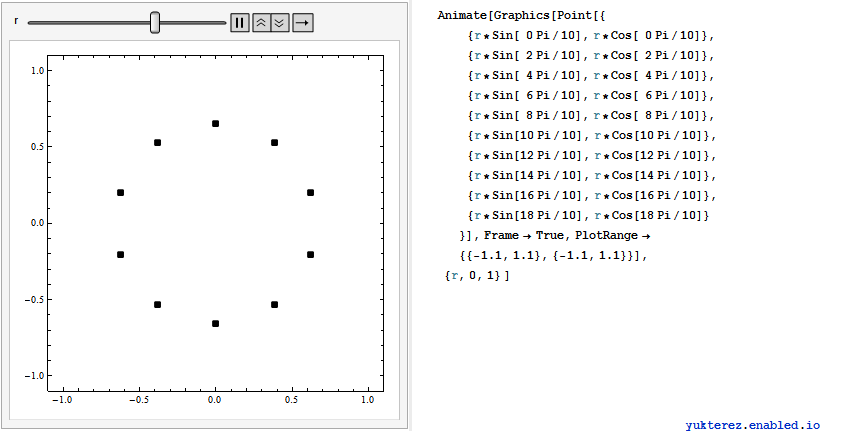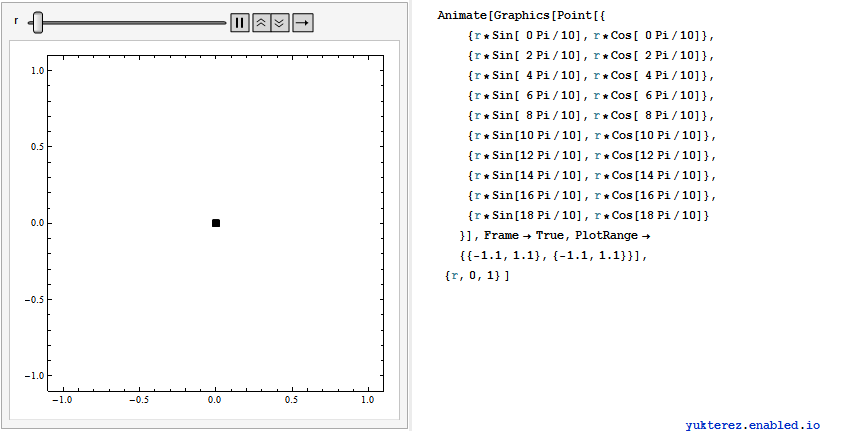








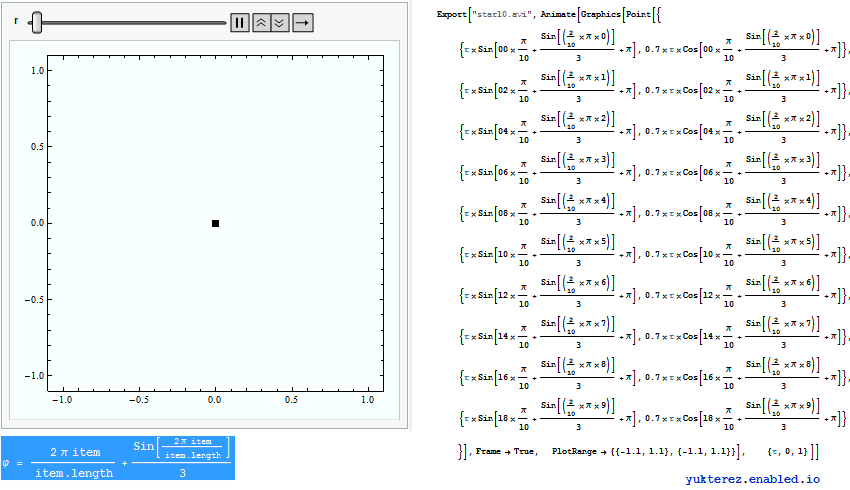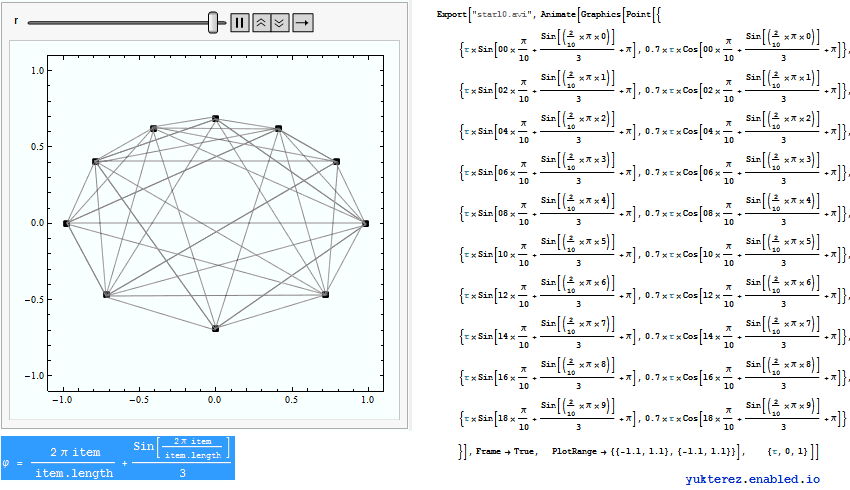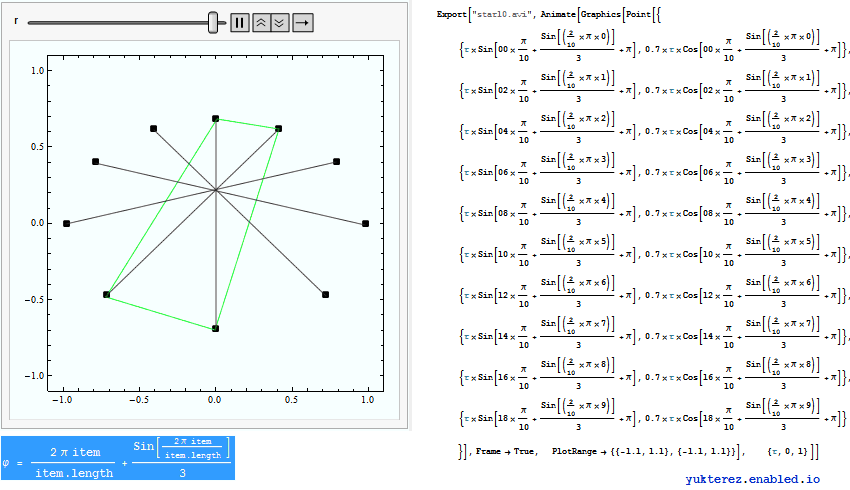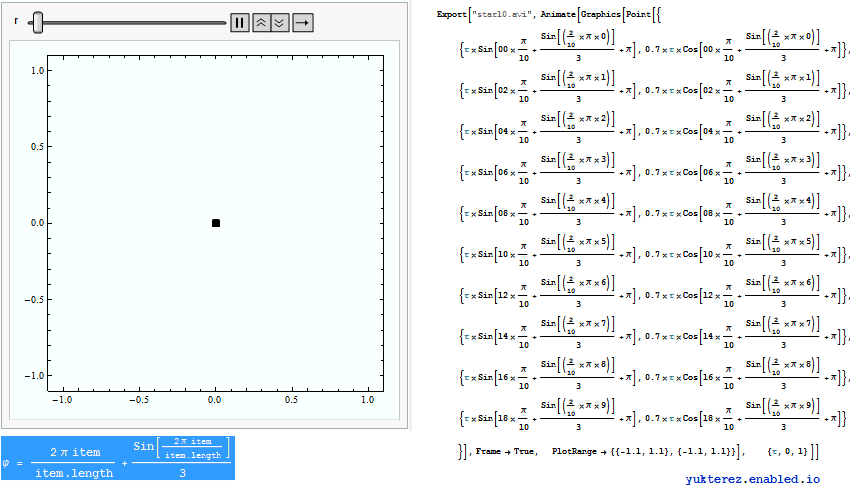







 , also erweitern wir auf
, also erweitern wir auf