
 Das ist die deutschsprachige Version.
Das ist die deutschsprachige Version.  English versions are available on en.yukterez.net and here.
English versions are available on en.yukterez.net and here.
Verwandte Beiträge: Kerr || Schwarzschild || De Sitter || Feldgleichungen || Gravitationslinsen || Raytracing || Paraboloid

 ←
←
Akkretionsscheibe um ein geladenes und rotierendes SL mit a=0.95, ℧=0.3, ri=isco, ra=10, Blickwinkel=89°. Erdoberfläche auf r=1.01r+.

 ←
←
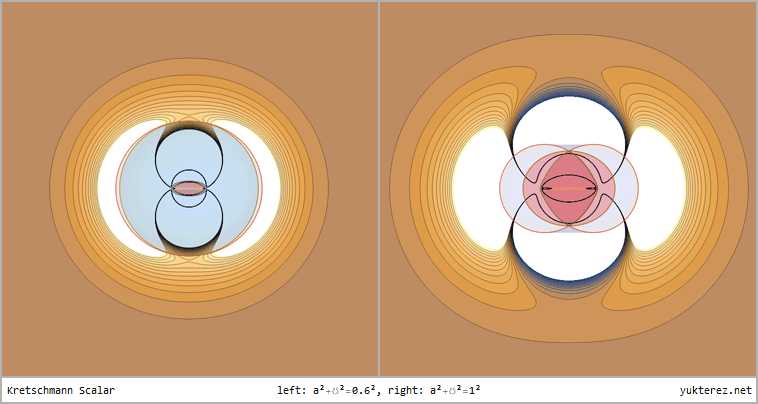
Kretschmann Skalar, kartesische Projektion, Blickwinkel=90°. Die Bereiche um die Pole sind negativ, und jene um den Äquator positiv gekrümmt.

 ←
←
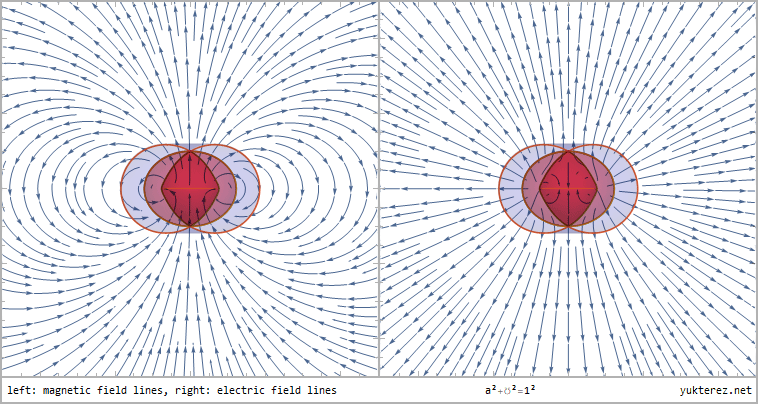
Magnetische (links) und elektrische (rechts) Feldlinien, kartesische Projektion, Blickwinkel=90° (edge on), Plotbereich=±5.

 ←
←
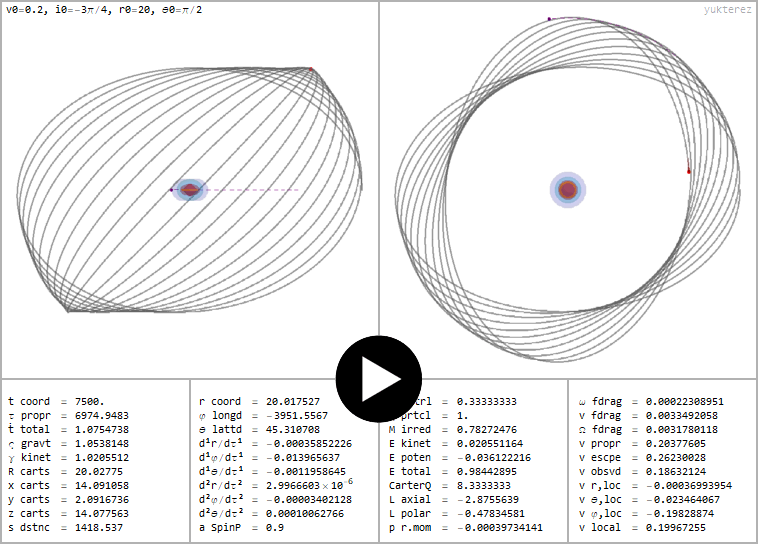
Retrograder Orbit eines mit q=1 geladenen Partikels um ein SL mit a=√¾ & ℧=⅓. v0 & i0: lokale Startgeschwindigkeit & Inklination
 ←
←
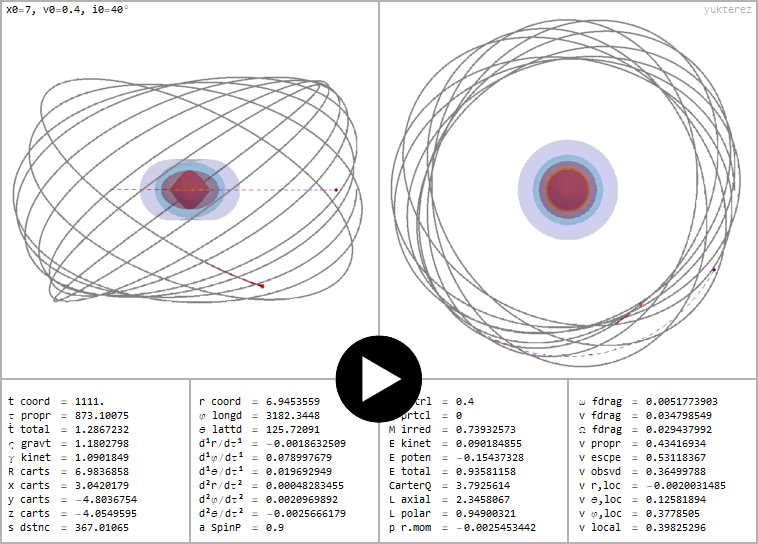
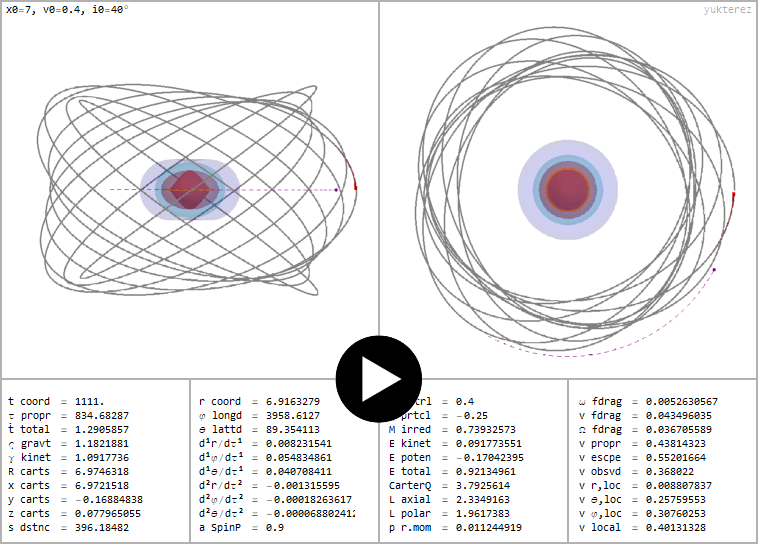
Prograder Orbit eines neutralen Testpartikels um ein mit a=0.9 rotierendes und ℧=0.4 elektrisch geladenes Kerr Newman SL
 ←
←
Prograder Orbit eines negativ geladenen Testpartikels (q=-¼) um ein wie oben rotierendes und positiv geladenes schwarzes Loch
 ←
←
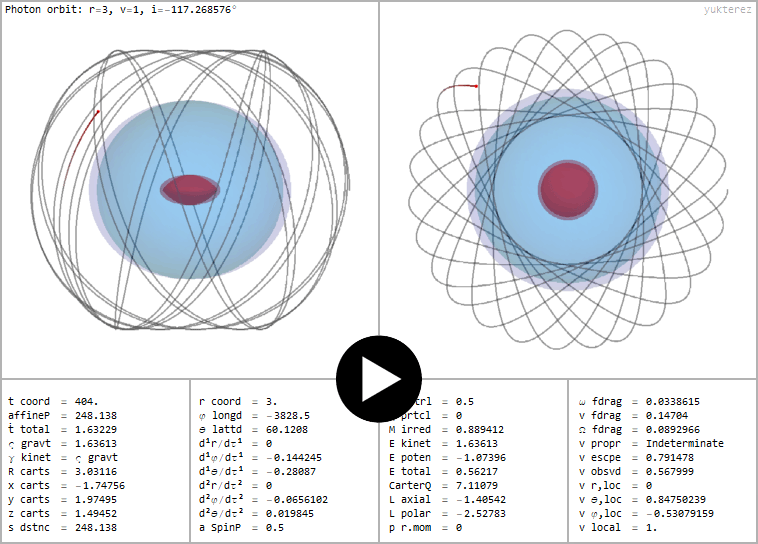
Nichtäquatorialer und retrograder Photonenorbit um ein mit a=½ und ℧=½ geladenes schwarzes Loch, konstanter Boyer Lindquist Radius
 ←
←
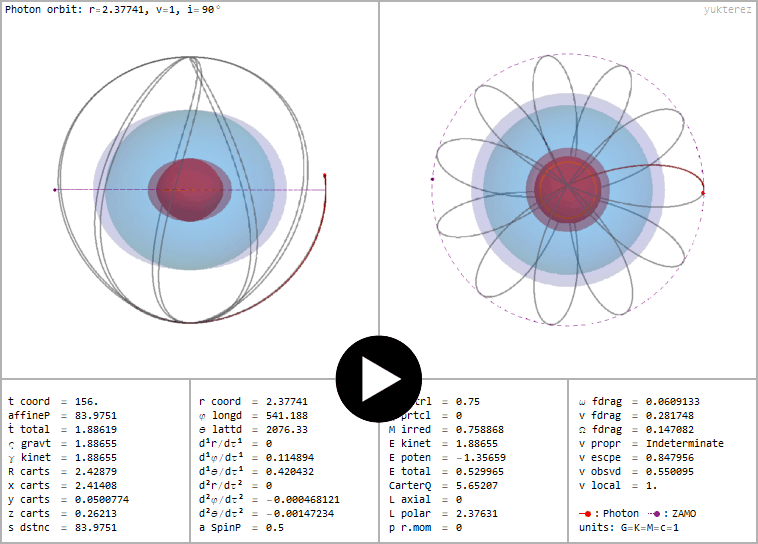
Polarer Photonenorbit (Lz=0) um ein mit a=½ rotierendes und mit ℧=¾ geladenes schwarzes Loch, konstanter Boyer Lindquist Radius
 ←
←
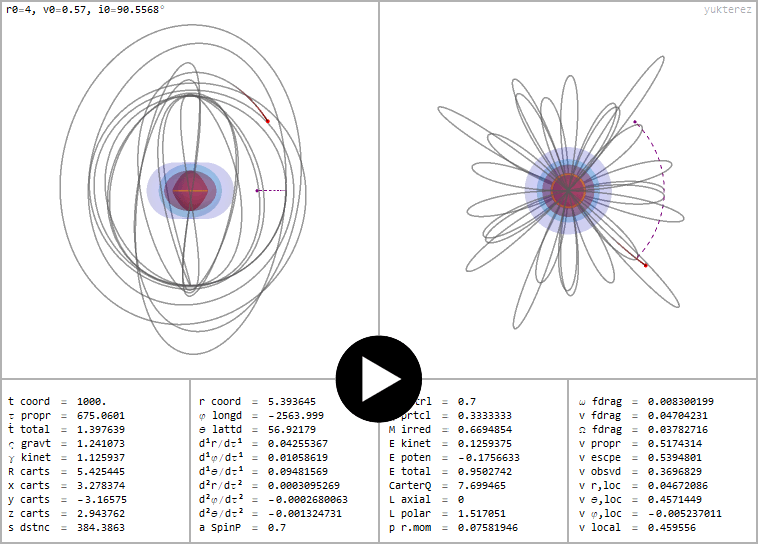
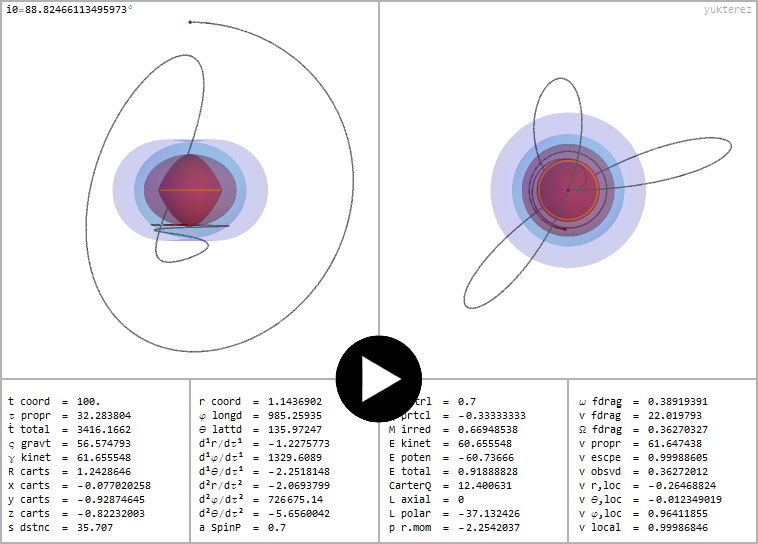
Polarer Orbit (Lz=0) eines positiv geladenen Testpartikels (q=⅓) um ein positiv geladenes und rotierendes schwarzes Loch (℧=a=0.7)
 ←
←
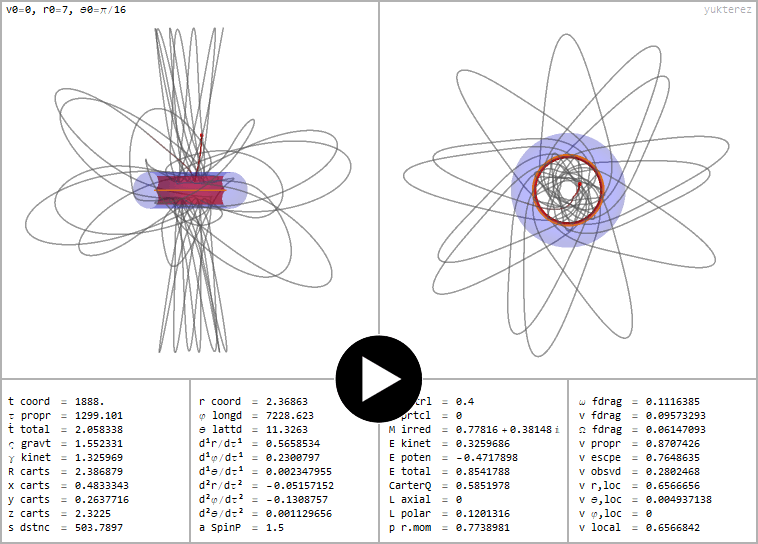
Plunge Orbit eines negativen Teilchens (q=-⅓), SL wie oben. Die Axialgeschwindigkeit bei q<0 ist für Lz=0 wegen der elektrischen Kraft positiv.
 ←
←
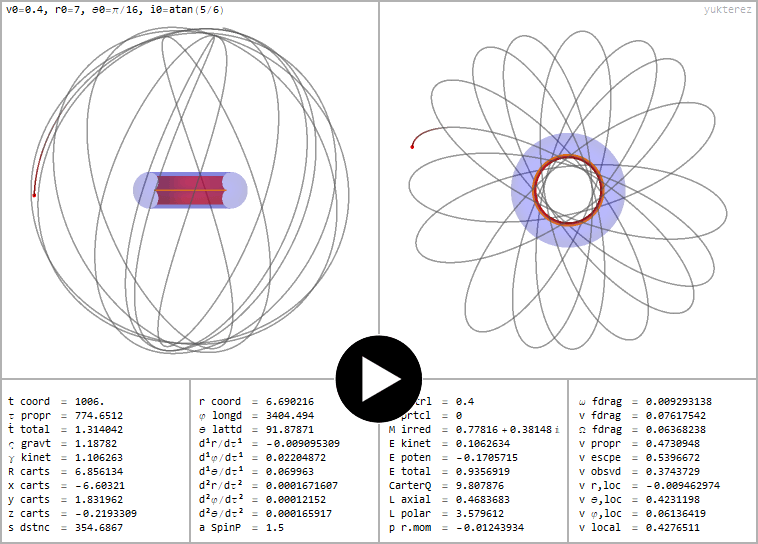
Freier Fall eines neutralen Testpartikels auf eine mit mit a=1.5 rotierende und und ℧=0.4 elektrisch geladene nackte Singularität
 ←
←
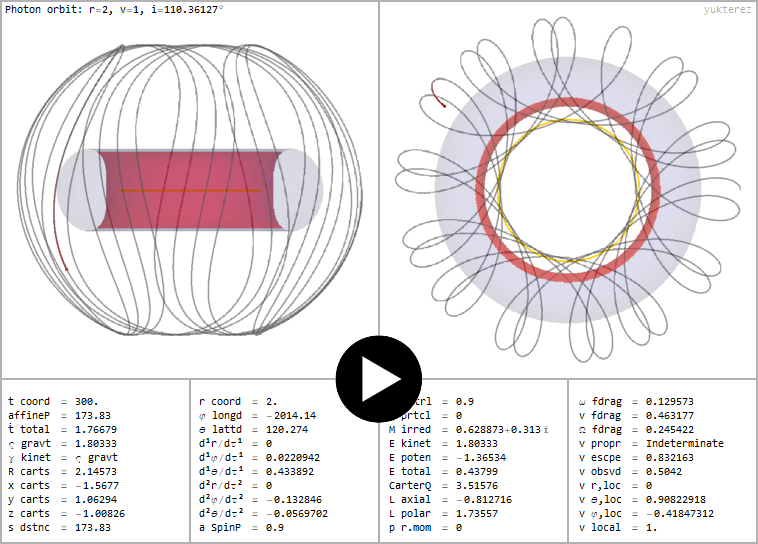
Geodätischer Orbit um eine nackte Singularität mit den gleichen Spin- und Ladungsparametern wie ein Beispiel weiter oben

 ←
←
Nichtäquatorialer und retrograder Photonenorbit um eine mit a=0.9 rotierende und ℧=0.9 geladene nackte Singularität

 ←
←
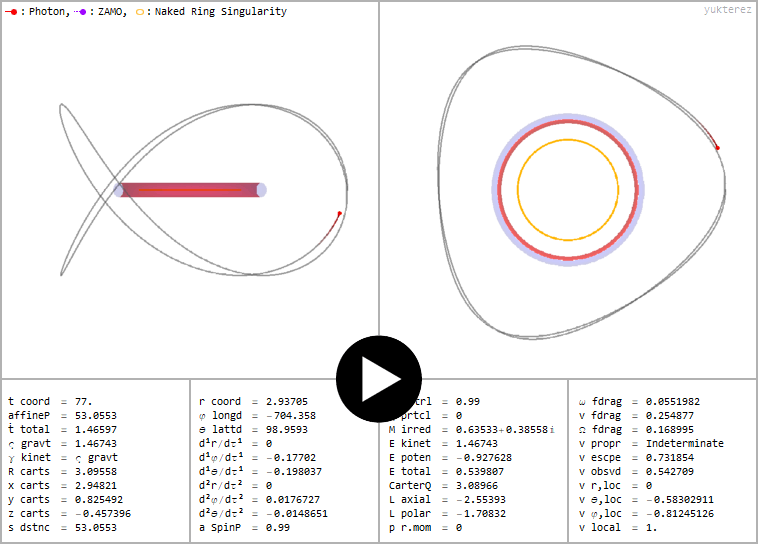
Retrograder Photonenorbit um eine nackte Singularität (a=0.99, ℧=0.99). Lokale äquatoriale Inklination: -2.5rad=-143.23945°

 ←
←
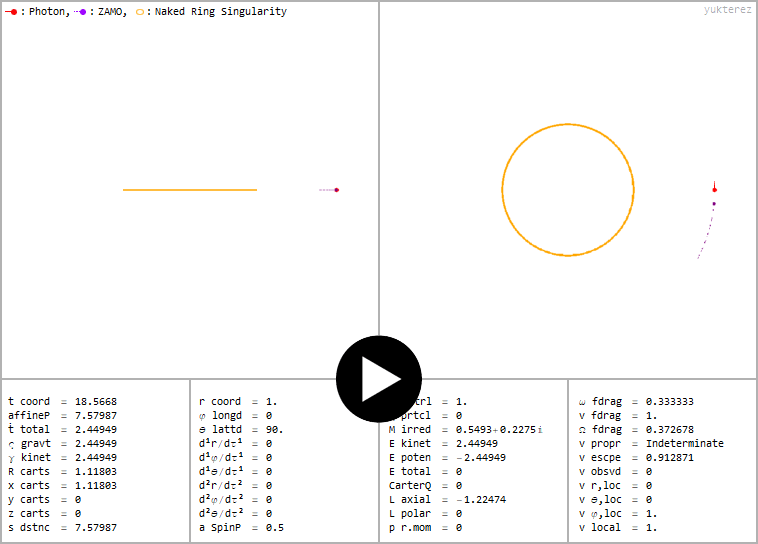
Stationärer Photonenorbit (E=0) um eine Ringsingularität (a=½, ℧=1). Außer bei r=1, θ=90° ist v framedrag überall <c, daher keine Ergosphären.
 ←
←
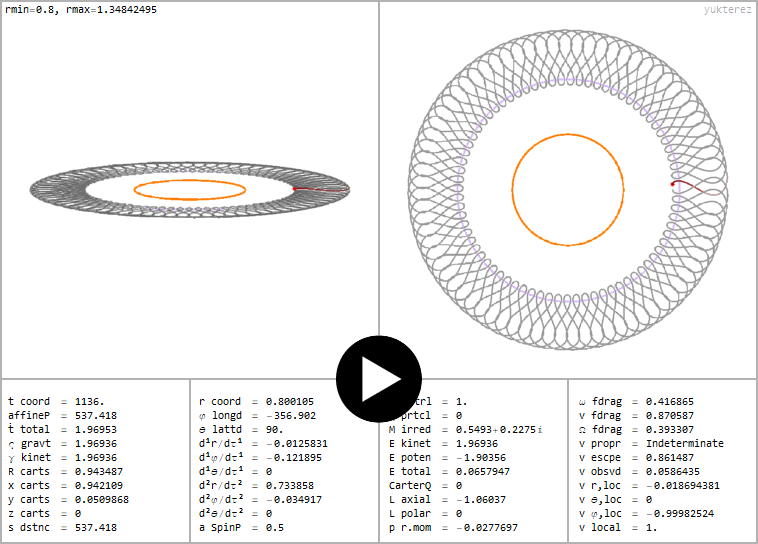
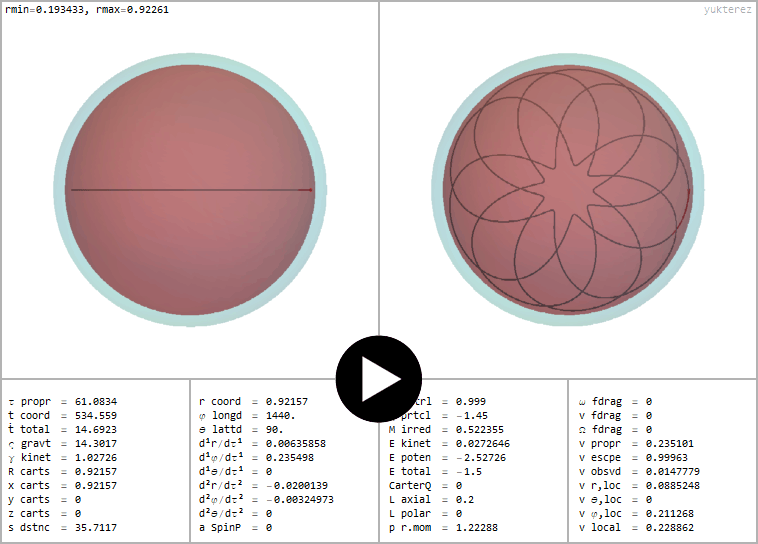
Äquatorialer retrograder Photonenorbit, Singularität bei r=0→R=√(r²+a²)=a=½. Ergoring (rosa) bei r=1, Umkehrpunkte bei r=0.8 und r=1.3484
 ←
←
Orbit eines negativ geladenen Partikels innerhalb des Cauchy Horizonts eines Reissner Nordström SL (vergleiche Dokuchaev, Fig. 1)

 ←
←Akkretionsscheibe um ein geladenes und rotierendes SL mit a=0.95, ℧=0.3, ri=isco, ra=10, Blickwinkel=89°. Erdoberfläche auf r=1.01r+.

 ←
←Kretschmann Skalar, kartesische Projektion, Blickwinkel=90°. Die Bereiche um die Pole sind negativ, und jene um den Äquator positiv gekrümmt.

 ←
←Magnetische (links) und elektrische (rechts) Feldlinien, kartesische Projektion, Blickwinkel=90° (edge on), Plotbereich=±5.

 ←
←Retrograder Orbit eines mit q=1 geladenen Partikels um ein SL mit a=√¾ & ℧=⅓. v0 & i0: lokale Startgeschwindigkeit & Inklination

 ←
←Prograder Orbit eines neutralen Testpartikels um ein mit a=0.9 rotierendes und ℧=0.4 elektrisch geladenes Kerr Newman SL

 ←
←Prograder Orbit eines negativ geladenen Testpartikels (q=-¼) um ein wie oben rotierendes und positiv geladenes schwarzes Loch

 ←
←Nichtäquatorialer und retrograder Photonenorbit um ein mit a=½ und ℧=½ geladenes schwarzes Loch, konstanter Boyer Lindquist Radius

 ←
←Polarer Photonenorbit (Lz=0) um ein mit a=½ rotierendes und mit ℧=¾ geladenes schwarzes Loch, konstanter Boyer Lindquist Radius

 ←
←Polarer Orbit (Lz=0) eines positiv geladenen Testpartikels (q=⅓) um ein positiv geladenes und rotierendes schwarzes Loch (℧=a=0.7)

 ←
←Plunge Orbit eines negativen Teilchens (q=-⅓), SL wie oben. Die Axialgeschwindigkeit bei q<0 ist für Lz=0 wegen der elektrischen Kraft positiv.

 ←
←Freier Fall eines neutralen Testpartikels auf eine mit mit a=1.5 rotierende und und ℧=0.4 elektrisch geladene nackte Singularität

 ←
←Geodätischer Orbit um eine nackte Singularität mit den gleichen Spin- und Ladungsparametern wie ein Beispiel weiter oben

 ←
←Nichtäquatorialer und retrograder Photonenorbit um eine mit a=0.9 rotierende und ℧=0.9 geladene nackte Singularität

 ←
←Retrograder Photonenorbit um eine nackte Singularität (a=0.99, ℧=0.99). Lokale äquatoriale Inklination: -2.5rad=-143.23945°

 ←
←Stationärer Photonenorbit (E=0) um eine Ringsingularität (a=½, ℧=1). Außer bei r=1, θ=90° ist v framedrag überall <c, daher keine Ergosphären.

 ←
←Äquatorialer retrograder Photonenorbit, Singularität bei r=0→R=√(r²+a²)=a=½. Ergoring (rosa) bei r=1, Umkehrpunkte bei r=0.8 und r=1.3484

 ←
←Orbit eines negativ geladenen Partikels innerhalb des Cauchy Horizonts eines Reissner Nordström SL (vergleiche Dokuchaev, Fig. 1)











































































