Code: Alles auswählen
m1 = 1; m2 = 1; r1 = 1; r2 = 1; r = 1.2 (r1 + r2); d = 5; T = 50; i = T/500;
g = 10; u1i = 9/10 Pi; u2i = 9/10 Pi; v1i = 0; v2i = 0;
sol = NDSolve[{
m2 r2 u2''[t] Cos[u1[t] - u2[t]] + (m1 + m2) r1 u1''[t] +
m2 r2 u2'[t]^2 Sin[u1[t] - u2[t]] + (m1 + m2) g Sin[u1[t]] == 0,
r2 u2''[t] + r1 u1''[t] Cos[u1[t] - u2[t]] -
r1 u1'[t]^2 Sin[u1[t] - u2[t]] + g Sin[u2[t]] == 0,
u1'[0] == v1i, u2'[0] == v2i,
u1[0] == u1i, u2[0] == u2i},
{u1, u2}, {t, 0, T},
WorkingPrecision -> MachinePrecision,
MaxSteps -> Infinity, Method -> Automatic,
InterpolationOrder -> All];
x[r_, u_, t_] := +r Sin[Evaluate[u[t] /. sol]][[1]];
y[r_, u_, t_] := -r Cos[Evaluate[u[t] /. sol]][[1]];
s[text_] := Style[text, FontSize -> font]; font = 11;
Quiet[Do[Print[Rasterize[Grid[{{Show[
Graphics[{Gray, Dashed, Circle[{0, 0}, r1]}, PlotRange -> {{-r, r}, {-r, r}}, Frame -> True, ImageSize -> 420],
Graphics[{Gray, Dashed, Circle[{0, 0}, r1 + r2]}],
Graphics[{PointSize[0.01], Black, Point[{0, 0}]}],
Graphics[{PointSize[(m1 + m2)/m2/100], Hue[0, 1, 0.5, 1], Point[{x[r1, u1, τ], y[r1, u1, τ]}]}],
Graphics[{PointSize[(m1 + m2)/m1/100], Hue[1/3, 1, 0.5, 1], Point[{x[r1, u1, τ] + x[r2, u2, τ], y[r1, u1, τ] + y[r2, u2, τ]}]}],
Graphics[{Gray, Line[{{0, 0}, {x[r1, u1, τ], y[r1, u1, τ]}}]}],
Graphics[{Gray, Line[{{x[r1, u1, τ], y[r1, u1, τ]}, {x[r1, u1, τ] + x[r2, u2, τ], y[r1, u1, τ] + y[r2, u2, τ]}}]}],
ParametricPlot[{x[r1, u1, t], y[r1, u1, t]}, {t, 0, τ}, ColorFunction -> Function[{x, y, t}, Hue[0, 1, 0.5, Max[Min[(-τ + (t + Min[d, τ]))/Min[d, τ], 1], 0]]], ColorFunctionScaling -> False],
ParametricPlot[{x[r1, u1, t] + x[r2, u2, t], y[r1, u1, t] + y[r2, u2, t]}, {t, 0, τ}, ColorFunction -> Function[{x, y, t}, Hue[1/3, 1, 0.5, Max[Min[(-τ + (t + Min[d, τ]))/Min[d, τ], 1], 0]]], ColorFunctionScaling -> False]]},
{s[" t" -> N[τ]]},
{s["x1"] -> s[N[x[r1, u1, τ]]]},
{s["y1"] -> s[N[y[r1, u1, τ]]]},
{s["x2"] -> s[N[x[r1, u1, τ] + x[r2, u2, τ]]]},
{s["y2"] -> s[N[y[r1, u1, τ] + y[r2, u2, τ]]]}},
Alignment -> Left]]],
{τ, i, T, i}]]Wenn die Animationen ruckeln einfach anklicken um sie einzeln abzuspielen.
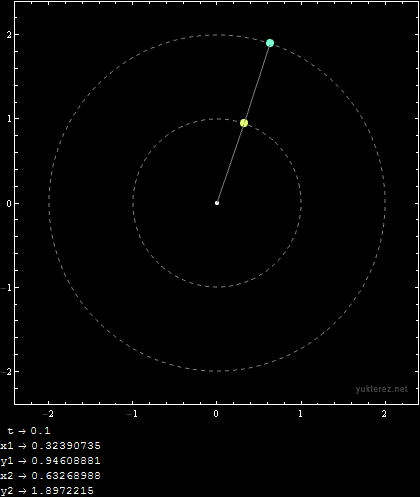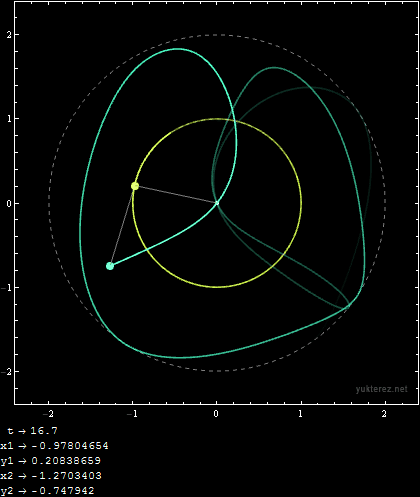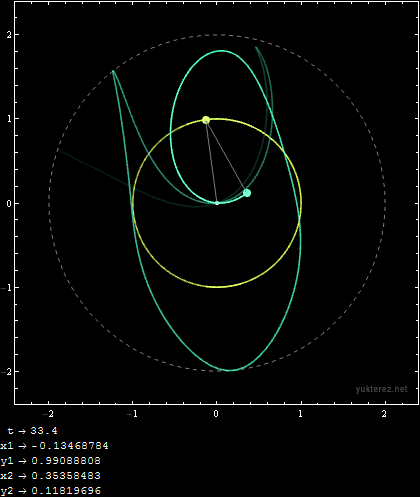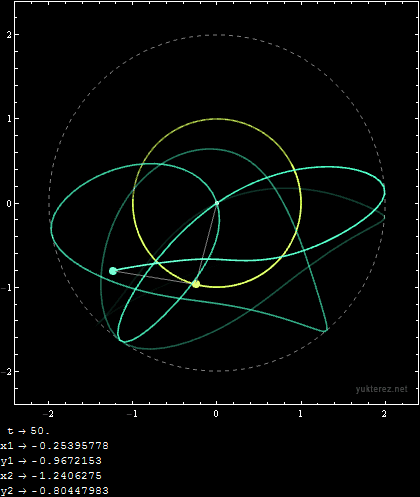
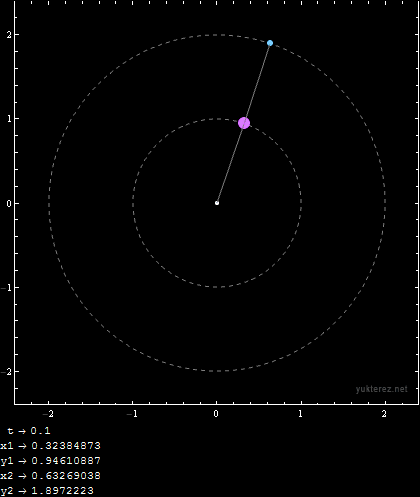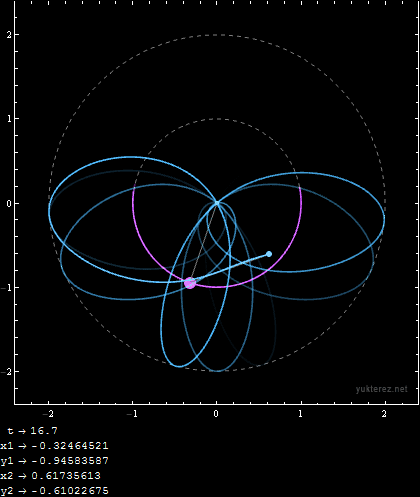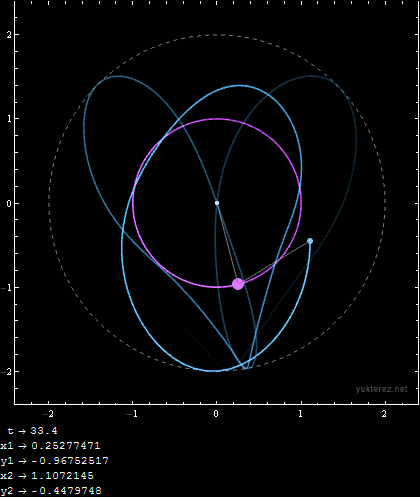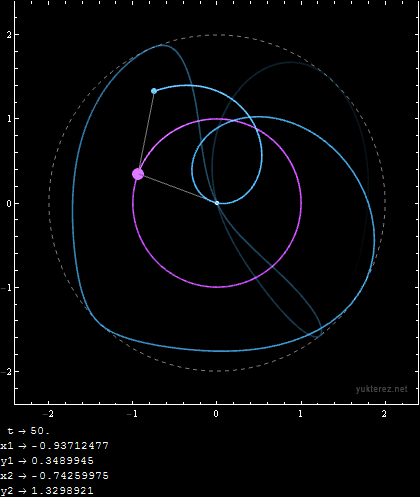
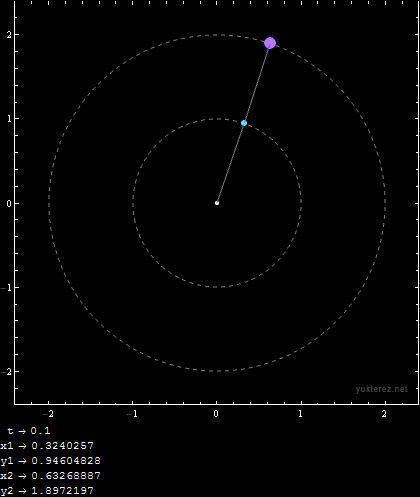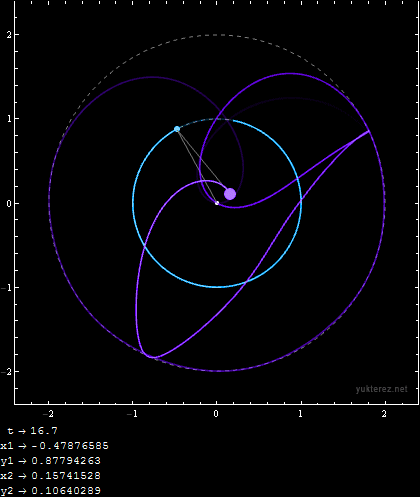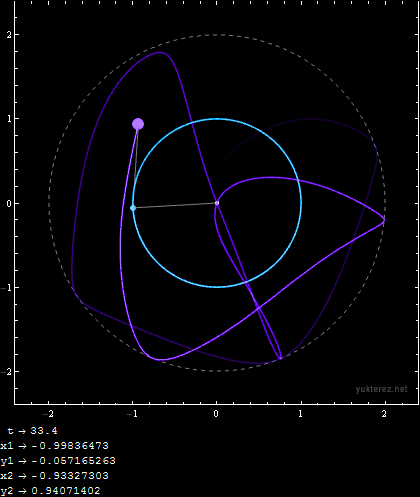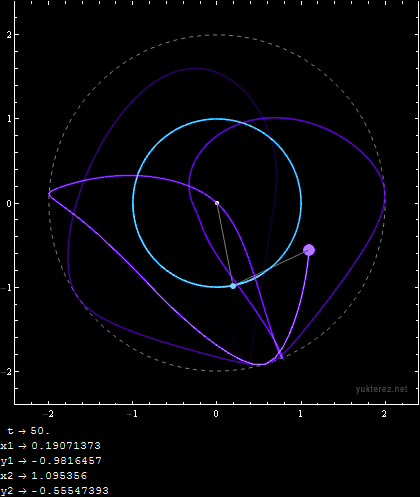
Initial Conditions:
m1 = 1; m2 = 1; r1 = 1; r2 = 1; u1i = 9/10 Pi; u2i = 9/10 Pi; v1i = 0; v2i = 0;
Initial Conditions:
m1 = 2; m2 = 1; r1 = 1; r2 = 1; u1i = 9/10 Pi; u2i = 9/10 Pi; v1i = 0; v2i = 0;
Initial Conditions:
m1 = 1; m2 = 2; r1 = 1; r2 = 1; u1i = 9/10 Pi; u2i = 9/10 Pi; v1i = 0; v2i = 0;
Initial Conditions:
m1 = 1; m2 = 1; r1 = 1; r2 = 1; u1i = 0; u2i = 0; v1i = 2; v2i = -2;

uni = Startwinkel von Pendel n in rad, yni = Startgeschwindigkeit von Pendel n in rad/sek
siehe auch: Einzelpendel


Animations by Simon Tyran, Vienna (Yukterez) - Creative Commons License CC BY-SA 4.0

