
 This is the english translation.
This is the english translation.  Die deutsche Version befindet sich auf pandemic.yukterez.net
Die deutsche Version befindet sich auf pandemic.yukterez.net
SIRD-Model

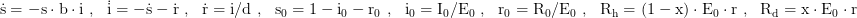
Initial conditions → E0: inhabitants, I0: infected, R0: recovered and immunized plus deceased, b0 and b1: initial and final transmission rate, b: time dependend transmission rate.
Parameters → T: timespan for the integration, tb: timespan for the change in the transmission rate, tu: timespan before the transmission rate starts to change, d: sickness duration, h: hospitalization rate, x: death rate, Rh: recovered and immunized, Rd: deceased.
The transmission rate can be larger that the effective spread rate; the first describes how many people per day on average receive a viral load from an infected person, while the latter says how many of those get indeed infected. If the product of the transmission rate and the sickness duration (the reproduction number ℛ=b·d) is smaller than 1 the number of infected people decreases over time, otherwise it increases.
Code: Alles auswählen
(* pandemic.yukterez.net *)
T = 300; (* Zeitraum *)
E0 = 83000000; (* Einwohner *)
I0 = 66; (* Infizierte *)
R0 = 0; (* Geheilte *)
b0 = 30/100; (* initiale Transmissionsrate *)
b1 = 30/100; (* finale Transmissionsrate *)
tu = 15; (* Zeitspanne der ungehinderten Ausbreitung *)
tb = 5; (* Zeitspanne b0 -> b1 *)
d = 30; (* Krankheitsdauer *)
h = 2/10; (* Hospitalisierungsrate *)
x = 3/100; (* Sterberate *)
f = (b0-b1)/tb; (* Änderung der Transmissionsrate *)
τ = t-tu;
B = If[b0==b1, b0, If[b1<b0, Max[b1, b0-f τ], Min[b1, b0-f τ]]];
b = Interpolation[Table[If[t<tu, b0, B], {t, 0, T, 1}]];
i0 = I0/E0; (* Fraktion der Angesteckten *)
r0 = R0/E0; (* Fraktion der Geheilten *)
s0 = 1-i0-r0; (* Fraktion der Ansteckbaren *)
DGL = {
s'[t] == -s[t] b[t] i[t], (* Änderungsrate der noch Gesunden *)
i'[t] == s[t] b[t] i[t]-i[t]/d, (* Änderungsrate der Infizierten *)
r'[t] == i[t]/d, (* Änderungsrate der Geheilten *)
s[0] == s0,
i[0] == i0,
r[0] == r0};
sol = Quiet[NDSolve[DGL, {s, i, r}, {t, 0, T+tu},
WorkingPrecision -> 48, MaxSteps -> Infinity,
InterpolationOrder -> All]];
max = Quiet[FindMaximum[i[t] /. sol, {t, 1}]]
Plot[{
Evaluate[E0 s[t] /. sol], (* noch gesund, rot *)
Evaluate[E0 i[t] /. sol], (* erkrankt, blau *)
Evaluate[h E0 i[t] /. sol], (* hospitalisiert, schwarz *)
Evaluate[(1-x) E0 r[t] /. sol], (* wieder gesund, grün *)
Evaluate[x E0 r[t] /. sol] (* gestorben, grau *)
}, {t, 0, T},
Frame -> True,
AxesOrigin -> {0, 0},
ImageSize -> 380,
PlotRange -> {All, {0, E0}},
ImagePadding -> {{50, 1}, {20, 10}},
PlotStyle -> {Red, Blue, Black, Green, Gray},
GridLines -> {{t/.max[[2]]}, {E0 max[[1]], E0/2}}]
Framed[Grid[Join[{{
"Tag ",
"Krank (N) ", "Krank (+%) ", "Tot ",
"Spital ", "Gesund ", "Genesen "
}}, {{" ", " ", " ", " ", " "}},
Table[{t,
Round[Evaluate[E0 i[t] /. sol][[1]]],
100 N[Evaluate[(i[t]/i[Max[0, t-1]]-1) /. sol][[1]], 4],
Round[Evaluate[x E0 r[t] /. sol][[1]]],
Round[Evaluate[h E0 i[t] /. sol][[1]]],
Round[Evaluate[E0 s[t] /. sol][[1]]],
Round[Evaluate[(1-x) E0 r[t] /. sol][[1]]]},
{t, 0, T, 1}]],
Alignment -> Left]]
Initial Conditions: Germany, February 29, 2020, best fit: here we assume that the lockdowns established on March 7 start to be effective after an average incubation delay of 1 week and decrease the intial transmission rate of 0.31 down to 0.15 within a period of 11 days in which the population gradually starts to obey the curfew. For a comparison with a constant transmission rate click here; plot:

x-axis: days; y-axis: persons, %; red: not infectected; blue: infected, black: hospitalized; green: recovered and immunized, gray: dead.
Coronavirus, Corona Virus, Covid-19, Sars-Cov-2, Equation, Formula, Exponential Growth, Pandemy Mathematics




