(* Input *)

    α = {0, -104} π/180;                                                     (* Singapur          *)    
    β = {+30, +95} π/180;                                                    (* Houston           *)   
    ψ = {+60, +25} π/180;                                                    (* Helsinki          *) 
    δ = {90, 0} π/180;                                                       (* Nordpol           *)   
    ω = 72921*^-9/sek;                                                       (* Erddrehung        *)    
    r = 6371000 m;                                                           (* Erdradius         *)    
    G = 667384*^-16 m^3 kg^-1 sek^-2;                                        (* Newtons Konstante *)    
    M = 5972 10^21 kg;                                                       (* Erdmasse          *)    
    c = 299792458 m/sek;                                                     (* Licht             *)    
   
    R = {-1.3, 1.3};                                                         (* Plotrange         *)    
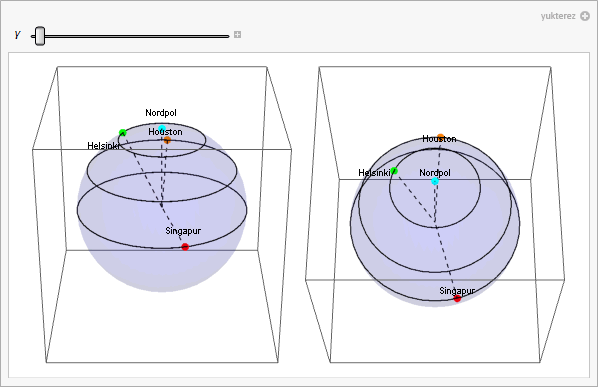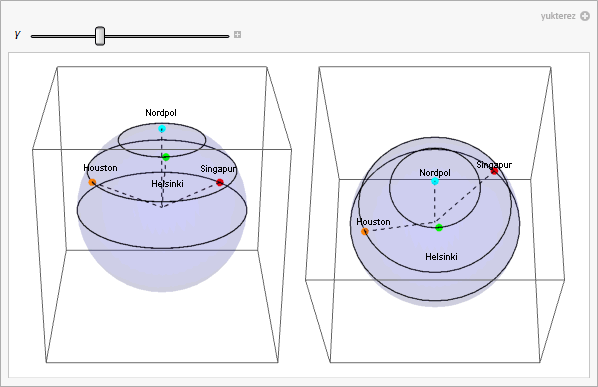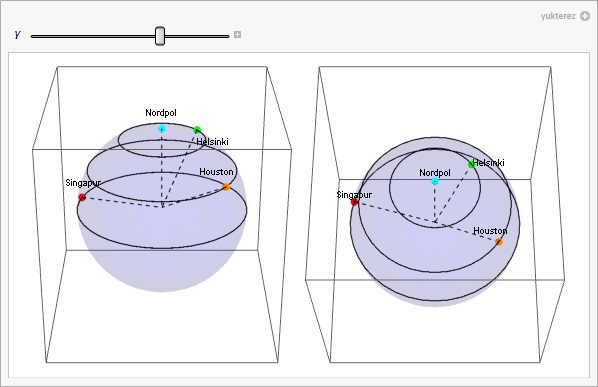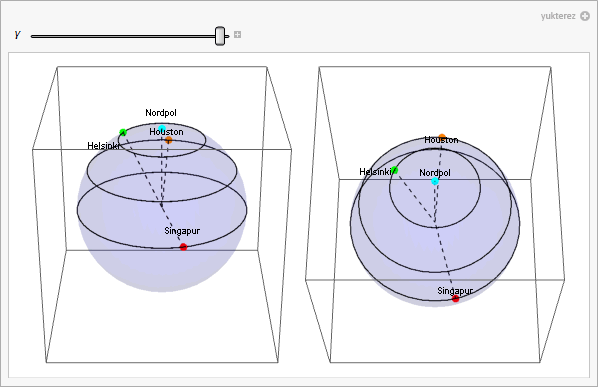
    P[ε_, γ_] := {Cos[γ]*Cos[ε], Sin[ε], Sin[γ]*Cos[ε]};                     (* Ortskoordinaten   *)
   
    export = Quiet[Manipulate[    
       plot[X_, Y_, Z_] :=    
        Graphics3D[{    
   
          {Opacity[0.1], Blue, Sphere[{0, 0, 0}, 1]},    
      
          {Red, PointSize[0.03], Point[P[α[[1]], γ + α[[2]]]]},     
           Text[StyleForm["Singapur", FontSize -> 9], {P[α[[1]] + 0.2, γ + α[[2]]]}],    
          {Dashed, Line[{P[α[[1]], γ + α[[2]]], {0, 0, 0}}]},    
      
          {Orange, PointSize[0.03],  Point[P[β[[1]], γ + β[[2]]]]},     
           Text[StyleForm["Houston", FontSize -> 9], {P[β[[1]] + 0.2, γ + β[[2]]]}],     
          {Dashed, Line[{P[β[[1]], γ + β[[2]]], {0, 0, 0}}]},    

          {Green, PointSize[0.03],  Point[P[ψ[[1]], γ + ψ[[2]]]]},     
           Text[StyleForm["Helsinki", FontSize -> 9], {P[β[[1]] + 0.2, γ + ψ[[2]]]}],     
          {Dashed, Line[{P[ψ[[1]], γ + ψ[[2]]], {0, 0, 0}}]},    
      
          {Cyan, PointSize[0.03],  Point[P[δ[[1]], γ + δ[[2]]]]},     
           Text[StyleForm["Nordpol", FontSize -> 9], {0, 1 + 0.2, 0}],     
          {Dashed, Line[{P[δ[[1]], γ + δ[[2]]], {0, 0, 0}}]},    
      
          {Opacity[0.01], Cylinder[{{0, Sin[α[[1]]], 0}, {0, Sin[α[[1]]] + 0.001, 0}}, Cos[α[[1]]]]},  
          {Opacity[0.01], Cylinder[{{0, Sin[β[[1]]], 0}, {0, Sin[β[[1]]] + 0.001, 0}}, Cos[β[[1]]]]},  
          {Opacity[0.01], Cylinder[{{0, Sin[ψ[[1]]], 0}, {0, Sin[ψ[[1]]] + 0.001, 0}}, Cos[ψ[[1]]]]},     
          {Opacity[0.01], Cylinder[{{0, Sin[δ[[1]]], 0}, {0, Sin[δ[[1]]] + 0.001, 0}}, Cos[δ[[1]]]]}}     
    ,
    ViewPoint -> {X, Y, Z},
    ImageSize -> 260,     
    PlotRange -> {R, R, R}];    
      
                                    p1 = plot[0, 2, -4]; p2 = plot[0, 4, -2];    
                                   {p1, p2}, {γ, 2 π, 0}, ControlPlacement -> Top]]   
     
    τg = Sqrt[1 - (2 G M)/(r c^2)]; τ[ε_] := Sqrt[1 - (ω Cos[ε] r)^2/c^2];    
   
   "t_Nordpol/t_Feldfrei" -> N[(τg τ[δ][[1]]), 16]
   "t_Äquator/t_Feldfrei" -> N[(τg τ[α][[1]]), 16]
   "t_Nordpol/t_Äquator"  -> N[(τg τ[δ[[1]]])/(τg τ[α[[1]]]), 16]


   (* Output *)

   

   t_Nordpol/t_Feldfrei -> 0.9999999993039402
   t_Äquator/t_Feldfrei -> 0.9999999993027394
   t_Nordpol/t_Äquator  -> 1.0000000000012007